这句话大家是不是最近已经要看吐了呢?
每当这个时候,就证明招聘旺季又来啦~
秋招、校招、社招……
那你真的准备好了吗?
现在程序员的面试,尤其是大厂程序员面试其实越来越看重算法基本功。所以想要去大厂,拿到一个心仪的offer,扎实的算法基本功必不可少。
今天牛牛就来跟大家来分享一个非常高频的算法面试题——LRU缓存淘汰算法。相信不少小伙伴在面试过程中都遇到过,这也是去年牛牛在腾讯三面时遇到的问题。
三面面试官上来首先天马行空地考察了一些基础的知识点,比如编程语言、常用中间件原理等等,虽然问题看起来简单,但咱也不能掉以轻心——这不是暗搓搓地对我们知识面广度的考察吗!接下来…相信认真读了牛牛上一篇文章的小伙伴也知道,就是redis缓存问题了!然而,你以为三面就这样结束了吗?不不不,还有LRU算法在等着你!
先别着急往下看,花个十秒钟想想,你觉得面试官会问你关于LRU的什么问题呢?
再花十秒钟问自己,这些问题你心中有答案吗?
下面牛牛就带大家走进面试现场,来一窥鹅厂面试官究竟考察了LRU的哪些知识点,看看和你想的是不是一样的。
LRU的应用场景
问:前面你对redis的一些存储原理答得还不错,那你知道redis的过期键清除策略和缓存淘汰策略吗?
答:过期键清除策略有三种:定时删除、定期删除以及惰性删除。redis过期键采用的是定期删除+惰性删除二者结合的方式进行删除的。redis的缓存淘汰策略则是采用LRU缓存淘汰算法。
从问题可以看出,在面试中,面试官通常不会一上来就要你手写一个LRU算法,往往是跟其他的知识点相结合,所以搞明白LRU的一些常用应用场景很重要。
亿点点细节,都问到算法相关的问题了,心里也要有点数了,手撕算法虽迟但到!
话说回来,其实不仅仅是在redis中有LRU的应用,在mysql中同样也有LRU的应用。
LRU在mysql中的应用就是Buffer Pool,也就是缓冲池。它的目的是为了减少磁盘IO(Input/Output),提高读取效率,所以当Buffer Pool满了的时候,也会采用LRU算法来清理缓存。但是不论是redis还是mysql都不是严格意义上的LRU算法,它们都是改进过后的近似LRU算法。你只要知道在mysql和redis中都有LRU的应用场景就好了。对其具体的算法感兴趣的小伙伴可以在留言区留言,牛牛将在后续文章中进行介绍。
LRU的含义
LRU的全称是Least Recently Used,即最近最少使用,也就是说我们认为最近使用过的数据应该是「有用的」,很久都没用过的数据应该是无用的,内存满了就优先删掉那些很久没用过的数据。
这里说句题外话,大家在面试时对于定义不必死记硬背,追求话术的专业性,一定要自己多思考多理解,能够表达清楚即可。
接下来想必大家也知道面试官要问什么了,对,就是LRU的实现方式。
LRU的实现方案
问:那你能谈谈你有哪些方法可以来实现 LRU 算法吗?
啊……关键问题来了,深吸一口气,咱们不要慌!
答:首先我们可以利用数组实现。这里我们可以用定长数组。
数组中的元素都有一个标记。这个标记可以是时间戳,也可以是一个自增的数字。
牛牛这里使用的就是后者——自增的数字。每放入一个元素,就把数组中已经存在的数据标记更新一下,进行自增。
当数组满了之后,就将数字最大的元素删除掉。每访问一个元素,就将被访问的元素数字置为0,而剩余未被访问到的元素自增1。这样标记最大的那个元素,就是最久未被使用过的元素,当数组满了,就删除这个最久未被使用过的元素。这里我们通过图示举个例子:
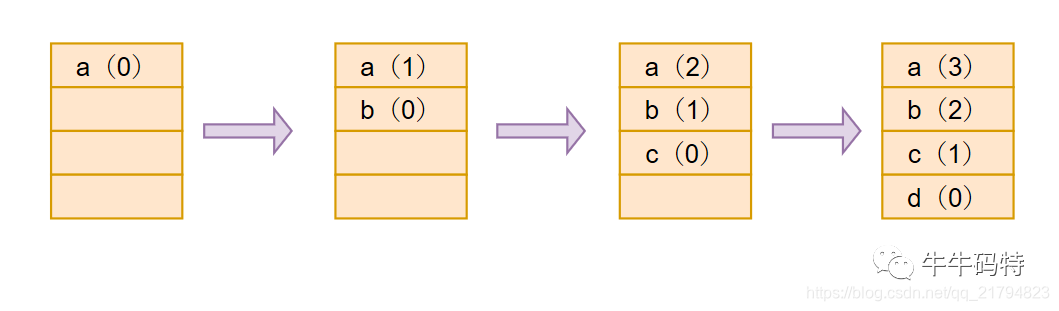
假设用一个长度为4的数组来实现这个结构,按照插入到数组的顺序,数组元素分别为a、b、c、d。
我们最先插入a,标记为0;再插入b,这时b的标记为0,数组中已有元素a自增1,a的标记变为1;再插入c,c的标记为0,数组中已有元素a和b的标记自增1,a的标记为2,b的标记为1。最后插入d,前面插入的元素均自增1,这时a就是最久未被使用过的元素。
假设此时我们访问到了元素b,则b的标记变为0,剩余元素标记自增1。

随后,假设又新来了个元素e要放入数组,则我们将标记最大的a删掉,在a的位置放入e,e的标记为0,其余元素标记自增1。

这样不就可以完美的实现淘汰最久没有被访问到的数据了吗,在面试场景中,采用数组存储也是最容易想到的。当然事情远没有想象的这么简单。这一种方案的弊端也是很明显:需要不停地维护数组中元素的标记。
牛牛自然知道这个方案,面试官肯定是不会满意的。因为,这不是最优方案也不是面试官想要的答案。但却是体现我们对这个题目思维过程的一个方式。
果然,面试官接着又问了。
问:那么你觉得它的时间复杂度是多少?
答:每次操作都伴随着一次遍历数组修改标记的操作,所以时间复杂度是 O(n)。
问:还有其他的方案吗
答:还有可以通过链表实现。
既然不用数组,又要找到一个最久未被使用过的数据,那么就要维护一个有序的数据结构。
我们可以用链表来存储,表头存放最久未被访问过的数据,表尾存放最近刚使用过的数据,当有一个数据被访问到,就将其移动至表尾。如果链表中没有该数据,当链表长度满了,就删除表头数据,插入该新数据到表尾,如果链表未满,就直接将该数据插入到表尾。
链表对于数据的插入、删除和移动都是O(1)时间的。看样子应该很完美了,但是其实要找到我们要访问的数据,这个查找过程还是不得不遍历数组,这个时间复杂度还是O(n)的。面试官自然不会就此罢休,所以……
问:你这个时间查询时间复杂度还是O(n)的,你能给一个查询和插入的时间复杂度都是O(1)的解决方案吗?
早知道有此一问,嘿嘿,牛牛自然也是有备而来,是时候拿出我们压箱底的方案了!!!
答:双向链表 + 哈希表!
方案要满足查询和插入的时间复杂度都是O(1)的要求,分解一下,也就是我们的方案需要满足以下几点:
1.这个结构必须是有序的,要能够找到最久未使用过的数据和最近使用过的数据;
2.要能在O(1)时间内完成数据的查询和插入;
3.要能快速移动元素,每次访问一个数据之后,要能变更这个数据的位置,将其放置到最近使用过的位置上,保证整个结构有序。
对于1和2,数据的快速查询和插入可以用哈希表,而对于3可以用链表实现,将他们综合综合一下,就能满足我们的需要了。得到一个新的数据结构:
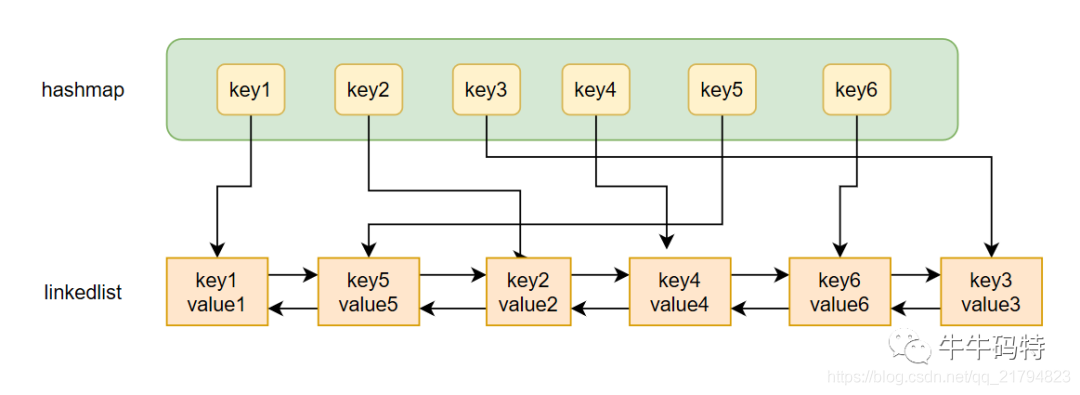
对于数据的查询,我们首先通过哈希表的key查找,快速定位到链表中的节点,从而取得对应的value;
对于数据的插入,每次都在链表尾部进行,直接在表尾插入数据,如果链表满了,则删除链表表头数据,再在表尾插入。所以链表表头存放着最久未被使用过的数据,表尾存放着最近使用过的数据;
对于数据更新,首先通过哈希表的key快速定位到需要更新的数据在链表中是哪个节点,然后通过修改指针,快速实现节点的位置变更。将最近访问过的节点移动到链表尾部。
讲到这里,面试官脸上总算露出了些许肯定的表情。
内心缓了口气,本以为到这里这个环节可以结束了,哪里料到面试官又追问了一句:
问:我看你实现的时候,是用的双向链表,那这个结构为什么要用双向链表呢,单链表为什么不行?
额....这个问题似曾相识,好像之前在某篇文章上看到过,但这会儿仿佛失忆了,就是想不起来。没办法,回忆不行,咱就只能自己现场分析思考了。
为什么单链表不行?
双向链表和单链表唯一的区别就是前者有一个前驱指针。有哪一个操作需要前向操作?嗯...对,就是删除元素!当我们要删除元素时,若为单链表则只能从表头开始遍历,才能找到要删除节点的前一个元素,并将其连接到它的后一个元素,这就是没有前驱指针的缺点,如果是双向链表,则可以在O(1)时间内定位到删除节点的前驱节点,大大提高了效率。
到这里我们的问题也找到了答案。
但,你以为终于可以结束了吗?天真!面试官的问题又随之而来了……
问:哈希表里面已经保存了key,链表中只存value不就行了吗,为什么还要同时存储key和value呢?
准备这道题的时候,只记得链表节点都是存储了key的,至于为什么要存储key,当时并没有深入思考。
key的作用是什么?——快速定位到数据的位置。
我们在哪几个地方用到了key?——哈希表结构中。
没错,所以这个问题的答案也在哈希表中。当链表满了我们需要删除表头数据来腾出空间,但是我们删除了链表里的元素,是不是还要删除对应的哈希表中的元素?要删除这个元素是不是要知道key是什么?这个key从哪里来?没错,key是从链表的节点里来的。
一波对比分析,问题是不是又迎刃而解了。
这里,牛牛也想告诉各位小伙伴,大家在面试的时候,遇到没有准备过的问题,或者是准备过但又想不起来了,duck不必慌张,一定要去思考问题的本质是什么,解铃还须系铃人,问题的本身才是关键,多反问自己为什么!
你往往会在一波反问和分析中得出惊喜的答案,即便没有得到答案也没关系,你要给面试官展示出对于问题的思考过程,这世上的难题那么多,就算是天才也不可能都有完美回答。
而且细心的小伙伴也应该发现了,其实面试官的问题也是循序渐进的,前面提出的问题也是在引导着你一步步去解决那个最终的问题。
面试官看中的往往是一个候选人对于问题的思考过程,以及这个人对问题的解决能力,而非答案本身。
回到面试现场——到这一步,面试官终于得到了满意的答案。不出意外,接下来就是紧张又刺激的手撕代码环节了。
问:那你能现场用这种方式实现吗?
其实关于面试过程中的手撕代码,我们没有办法逃避,也没有过多的技巧或面经,唯一的方法只有多练、多刷题,量变引起质变,当刷够了一些常用算法题之后,我们对于算法的理解自然会提升一个高度,在面试中也会不那么慌张,显得游刃有余。
好了,这次关于LRU的算法面试,就为大家分享到这里,校招将近,也预祝大家都能早日拿到一个满意的offer。